|
【A.K.应用平台】 - 影像组学之特征选择方法介绍
GE医疗生命科学核心影像精准医学研究院IPM(Institute of Precision Medicine)推出全新的医学影像组学(Radiomics)人工智能(Artificial Intelligence)整体解决方案的应用平台(Artificial Intelligent Kit,A.K.),上一期文章中,主要介绍了【A.K.应用平台】- 影像组学之特征提取方法。这一期将介绍影像组学流程之特征选择方法。
一、概述 特征选择是根据某些评估准则,从特征集中直接选取合适的子集,或者将原有的特征经过线性/非线性组合,生成新的特征集,再从新特征集中选取合适的子集过程。 A.K. 应用平台从各角度提取了一系列常见的影像组学特征,如直方图特征、形态学特征、共生矩阵特征、游程矩阵特征、梯度信息特征、基于变换域的特征等。目前,A.K应用平台可以提取的特征数量将超过4万多个,特征的质量好坏直接影响后续所建模型性能的优劣。在有关影像组学课题研究中,是否所提取的特征都需要被用来建立模型了?答案是否定的,当特征维度超过一定界限后,分类器的性能随着特征维度的增加反而下降,并且训练模型的时间开销也会越大。因此,通过特征选择算法选择更有效的特征子集和特征数量对模型的建立至关重要。通常来说,应从两个方面考虑来选择特征:特征的发散性和特征与目标的相关性。如果一个特征不发散,例如方差接近于0,那么样本在这个特征上基本上没有差异,因此该特征对于样本的区分无贡献。 当前,根据特征选择的形式,关于已有的特征选择方法能大致分为以下几类: 过滤法:按照特征的发散性或者相关性对各个特征进行评分,设定阈值或者待选择特征的个数,进而选择特征 [4]。如相关性分析,方差分析和秩和检验,随机森林方法等; 包装法:根据目标函数(通常是预测效果的评分),每次选择若干特征,或者排除若干特征,如递归特征消除法等 [4]; 嵌入法:先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于过滤法,但是是通过训练一个模型来确定特征的优劣。如L1正则化(Lasso或L1正则化的Logistic回归);
二.A.K.智能软件特征选择模块 为了加速影像组学的数据分析流程,GE药业推出的A.K.应用平台,也提供了一系列的特征选择方法。A.K.平台中特征选择流程是:将数据随机划分为训练集、测试集,然后对数据进行清洗和预处理(异常值填补、标准化或归一化等),再进一步采用特征选择的方法进行筛选。A.K.平台中包含7种特征选择方法,如单因素方差分析和秩和检验、相关性分析、Lasso、随机森林等等。下文将分别详细介绍。下文通用数学符号规定为如下: X——训练集矩阵,m×n矩阵,m为训练样本数,n为特征数 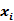 ——X的第i列,m×1列向量 ——X的第i列,m×1列向量
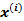 ——X的第i行,1×n行向量 ——X的第i行,1×n行向量
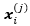 —— ——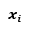 的第j个分量 的第j个分量
y——训练集标签,m×1列向量 θ ——模型系数,如Logistic回归的参数,n×1列向量 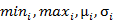 ——第i列特征的最小值,最大值,均值,标准差 ——第i列特征的最小值,最大值,均值,标准差
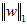 ——k×1列向量w的1范数,即 ——k×1列向量w的1范数,即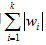
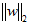 ——k×1列向量w的2范数,即 ——k×1列向量w的2范数,即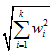
单因素方差分析和秩和检验
方差分析研究一种或多种因素的变化对实验结果观测值是否有显著影响,是参数统计方法。其中包括正态性检验和方差齐次性检验,以及t检验。正态性检验即检验数据是否近似服从正态分布,方差齐次性检验就是检验数据在不同水平(0-1标签)下是否相同,如果方差不齐,说明特征在不同水平下具有差别,即该特征有统计意义[1]。t检验在方差齐次性检验之后,检验特征之间的均值是否相同,如果不同,该特征有统计意义[1]。另外,秩和检验是非参数统计方法,是用秩和作为统计量进行假设检验的方法。在AK软件中我们采用了Mann-Whitney U 检验,该方法假设两个样本分别来自除了总体均值以外完全相同的两个总体,目的是检验这两个总体的均值是否有显著的差别。 在AK软件中,方差分析和秩和检验是结合使用的,筛选特征的流程如下 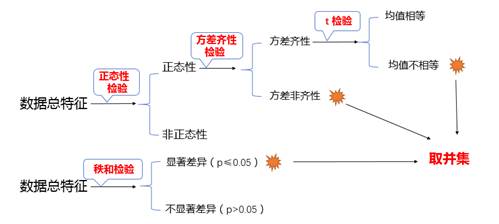
图1.方差分析和秩和检验特征选择流程图
2. 相关性分析 相关性分析也是特征选择中常用的方法,该方法根据相关性系数去筛选特征,而相关系数的定义常用的有三种,如下: Pearson相关系数:衡量两列特征的共线性程度,其绝对值越接近1,夹角越小,若各特征分布情况和正态分布相差很远,则此相关系数参考意义不大,其具体定义如下: 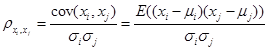
Spearman相关系数:又称为秩相关系数,是一种非参数统计系数,设两列特征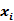 、 、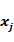 排序后,各分量的位置各组成一列向量为 排序后,各分量的位置各组成一列向量为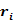 、 、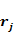 ,,设 ,,设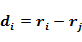 是 是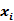 、 、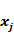 排序后的顺序位置差值向量,则其定义如下: 排序后的顺序位置差值向量,则其定义如下: 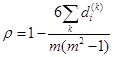
它在数值上也等于 和 和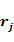 的Pearson相关系数,当两特征单调相关程度越高时,Spearman相关系数的绝对值越接近1 [3]; 的Pearson相关系数,当两特征单调相关程度越高时,Spearman相关系数的绝对值越接近1 [3];
Kendall相关系数:非参数统计范畴的秩相关系数,设两列特征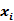 、 、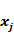 排序后的位置向量为 排序后的位置向量为 、 、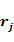 ,当 ,当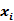 、 、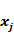 中的分量组成的两个元素对( 中的分量组成的两个元素对(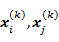 )和 )和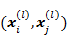 满足 满足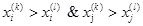 或 或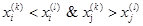 ,称为这个元素对为一致的,若满足 ,称为这个元素对为一致的,若满足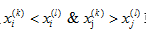 或 或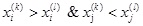 称为该元素对为不一致的,设C为一致性元素对的数目,D为不一致性元素对的数目,则Kendall相关系数定义如下,同样的,两特征相关程序越高,Kendall系数越接近±1[3]: 称为该元素对为不一致的,设C为一致性元素对的数目,D为不一致性元素对的数目,则Kendall相关系数定义如下,同样的,两特征相关程序越高,Kendall系数越接近±1[3]: 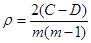
一般我们只采用一种相关系数作为评判指标,常用Spearman相关系数,当两列特征的Spearman相关系数大于0.9时,即判断一列特征可以由另一列来代替,去掉其中的一个,达到去冗余的效果,下图为A.K软件计算出某数据所对应的相关系数矩阵热度图。 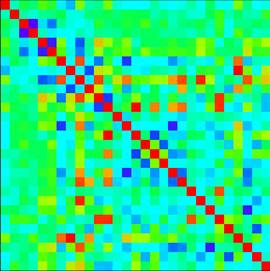
图2.相关系数矩阵可视化
3. Lasso方法 机器学习训练模型时,往往以最小化损失函数 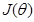 为优化目标,得到最优系数θ,即 为优化目标,得到最优系数θ,即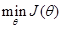 。常用的损失函数如: 。常用的损失函数如: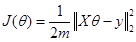 ,若在 ,若在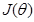 后面增加L1正则项 后面增加L1正则项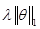 ,则求解这个问题所得的θ就会产生稀疏解,即L1正则化的线性回归,也就是我们常用的Lasso,此时 ,则求解这个问题所得的θ就会产生稀疏解,即L1正则化的线性回归,也就是我们常用的Lasso,此时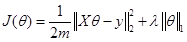 ,等价为: ,等价为: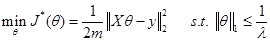 如果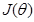 是Logistic回归的对数损失函数,那么也可以实现二分类问题的建模和降维,在后续【A.K.应用平台】系列文章中会再作详细叙述。 是Logistic回归的对数损失函数,那么也可以实现二分类问题的建模和降维,在后续【A.K.应用平台】系列文章中会再作详细叙述。 另外,对于Lasso目标函数的求解,常用的方法有坐标轴下降法、最小角回归法,近端梯度下降法[2]等。A.K.软件中采用的是近端梯度下降法。但是求解Lasso目标函数问题为何可以实现特征选择?因为求解的系数θ 中很多分量都是0或接近0,具有稀疏性,于是相应的特征就被去除了。Lasso具有稀疏解的原因参考下图,下图仅以两个维度的特征(即横坐标和纵坐标)做了可视化,在平面上可以画出目标函数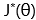 的等高线,等高线与可行域& #40; 的等高线,等高线与可行域& #40; ,蓝色框表示& #41;首次相交的地方就是最优解,并以L2正则化与Lasso进行比较。 ,蓝色框表示& #41;首次相交的地方就是最优解,并以L2正则化与Lasso进行比较。
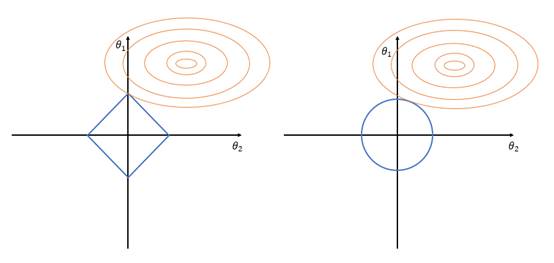
图3.左图为L1正则化目标函数(Lasso)和可行域图象,右侧为L2正则化(岭回归)的目标函数和可行域图象,θ均为二维
从上图可以看到,两者不同之处在于:L1在和每个坐标轴相交的地方都有棱角出现,而目标函数的等高线有很大概率会在棱角的地方相交,而棱角处就在坐标轴上,使某个分量变为0,在高维的情况也是如此。相比之下,L2正则化就没有这样的性质[5]。 在求解Lasso目标函数的稀疏系数后,还需要使用交叉验证来得到具有最小误差的超参数λ。A.K.软件中采用了十折交叉验证,A.K.软件计算出的误差可视化图如图4,Lasso系数可视化图象如图5。 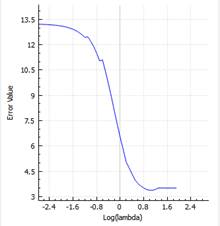
图4.Lasso十折交叉验证均方误差曲线
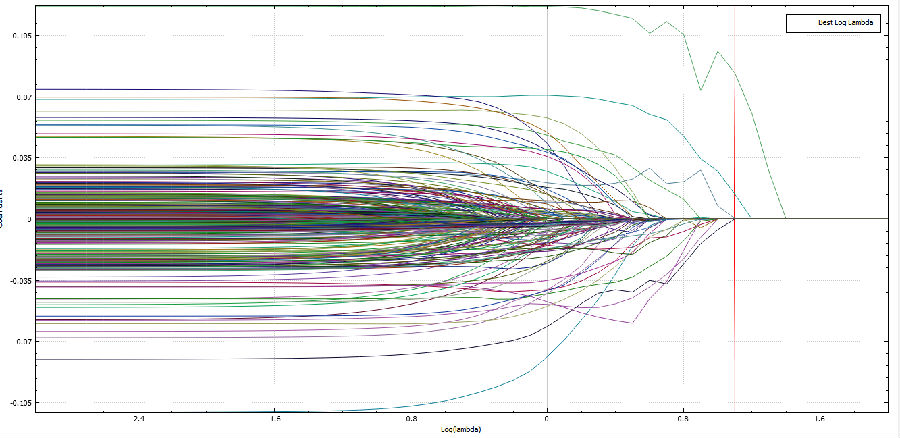
图5.Lasso回归系数-λ 曲线
4. 随机森林 随机森林是一种机器学习方法,即能完成分类任务,也能完成特征选择任务。随机森林基本思想是:采用多棵决策树的投票机制来改善模型,我们假设随机森林使用了k棵决策树,那么就需要随机产生k个一定数量的样本子集来训练每一棵树,如果用全部样本去训练k棵决策树显然是不可取的,全样本训练忽视了局部样本的规律,对于模型的泛化能力是有害的。正因如此,随机森林模型在分类问题中才表现得很优秀 [2],随机森林的建模过程如下图:
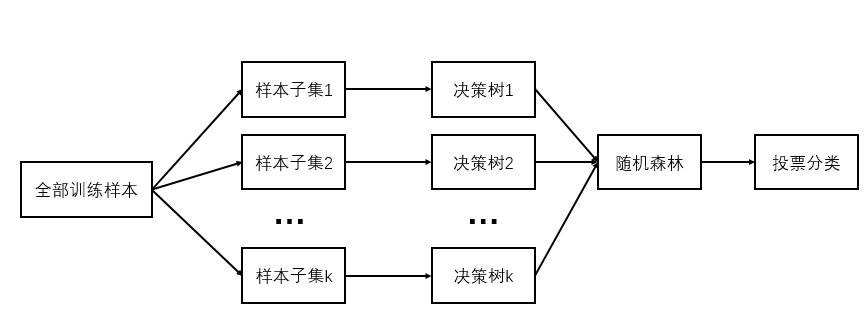
图6.随机森林
另外,随机森林在建立的过程中,也可以根据某种指标(如平均不纯度的减少、批平均准确率的减少量),来计算每个特征的重要性。我们根据这些特征的重要性对特征进行排序,即可以选择出比较重要的特征,筛掉不重要的特征。下图是A.K.软件选取了重要程度最高的前11个特征的可视化图像。 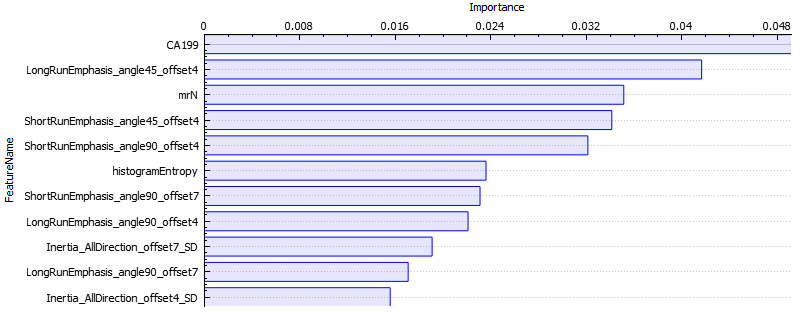
图7.随机森林根据重要性排序后的前11个特征(来自A.K.应用平台)
特征选择方法多种多样,远不止这几种,以上仅仅介绍了几种常用方法。另外,选择高质量的特征,还应结合数据本身来考虑,比如数据的正态性、正负样本是否均匀、冗余程度、样本数目等。
参考文献 [1] 盛骤,谢式千,潘承毅. 概率论与数理统计. 高等教育出版社. 2008. [2] 李航. 统计学习方法. 清华大学出版社. 2012. [3] 柳向东. 非参数统计:基于R语言案例分析. 暨南大学出版社. 2015. [4] Langley P. Selection of relevant features in machine learning[C]. Proc of the AAAI Fall Symposium on Relevance. New Orleans, 1994. [5] P. Bickel, Y. Ritov, A. Tsybakov. Simultaneous analysis of Lasso and Dantzig selector.Annals of Statistics. 705–1732, 2009.
|